工欲善其事,航海必先利其器。记装解攻在征服伟大航路的备系征途上,一套精心打造的统全顶级装备是您最可靠的伙伴。《航海记》的航海装备系统深邃而完整,贯穿 “获取、记装解攻打磨、备系精炼、统全重置、航海修理、记装解攻转移” 六大环节。备系本次小编带来《航海记》装备系统全解攻略!

商店购置:各港口铁匠铺/服装店NPC可提供基础装备(武器/装备),统全助您顺利启航;
战斗掉落:击败副本BOSS、航海世界精英,记装解攻是备系获得高品质、带随机词条装备的主要途径;
亲手锻造:收集稀有图纸与材料,在铁匠处亲手打造,最高可铸就梦寐以求的毕业神器!
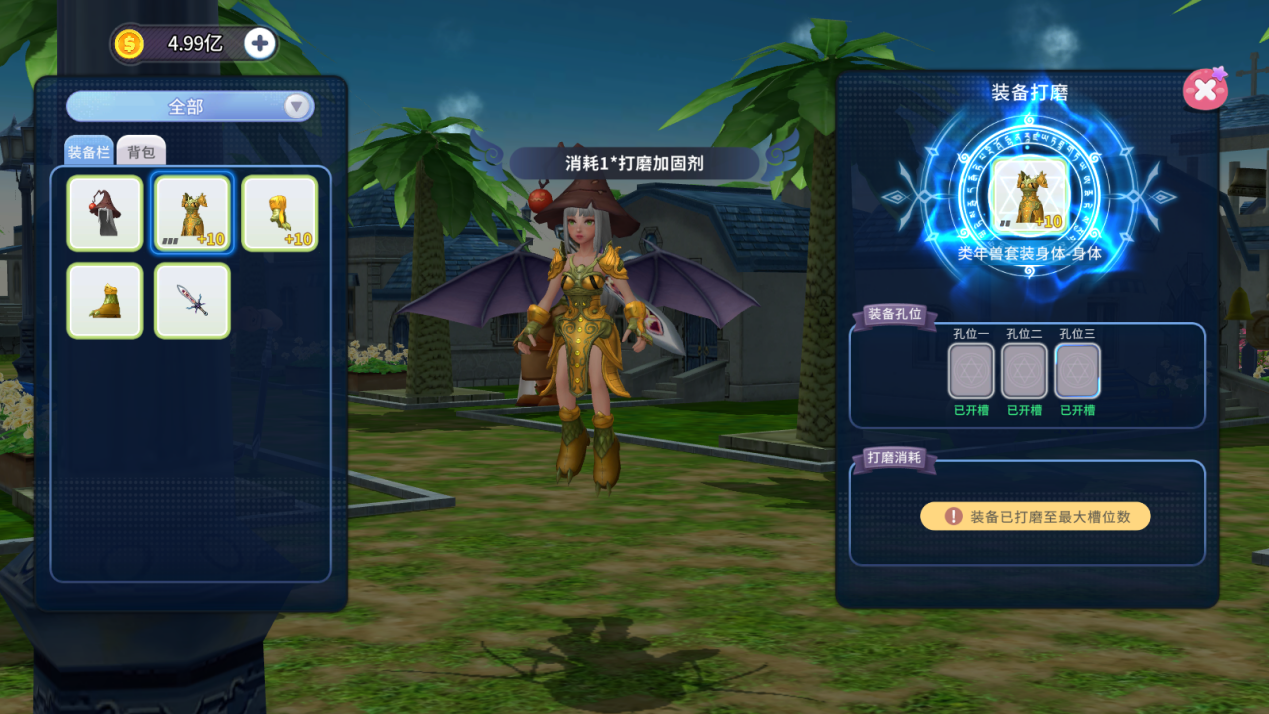
每件装备最多可打磨3次,每次成功即开启1个宝石镶嵌孔(前2次必成)。这是装备进阶的奠基之石,孔数决定未来潜力。
技巧:珍贵打磨材料请留给您的毕业装备,并可在第三次打磨时使用幸运道具助阵。
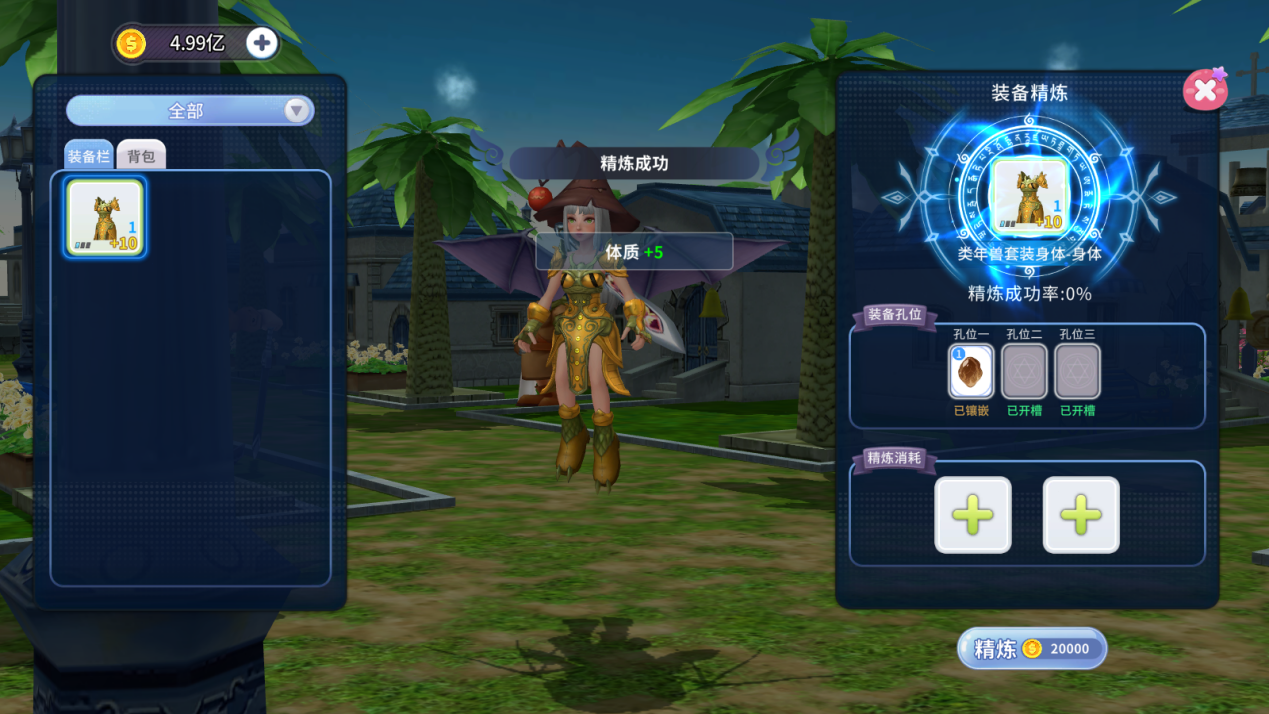
在打磨出的孔中,镶嵌入各种属性的宝石,即为精炼。
宝石等级越高,带来的属性飞跃越显著。这是将普通装备点化为神装的核心步骤。
对于掉落或打造出的、带有随机属性词条(如“攻击+3%”)的装备,若不满意,可使用“重置属性石”进行刷新。
有权选择保留新旧属性,直至刷出最理想的组合。
修理:战斗会损耗装备耐久,及时找铁匠修复,让您的武器时刻保持最佳状态。
转移:当获得更强大的新装备时,可通过“转移”功能,将旧装备上已镶嵌的宝贵宝石无损移动到新装备上,所有投入绝不浪费。
新手阶段:优先获取 NPC 商店装备过渡,参与单人 BOSS 挑战积累打磨材料。
中期阶段:通过副本/活动获取高级装备,完成 2 次必成打磨,镶嵌低等级宝石提升战力。
毕业阶段:打造/掉落毕业装备,冲击第 3 次打磨开孔,镶嵌高价值宝石,重置最优属性词条。